Why is optimization important?
A business owner would say: 1. To minimize cost. 2. To maximize profit. Obviously there can be other goals in mind that are not related to balance sheets. For example, an engineer may want to maximize heat transfer, minimize server load, minimize production time, maximize validation accuracy, etc. Whatever the case may be, optimization is an essential step to maximize the success of any process. Notice that in some situations minimizing certain factors actually maximizes the desired outcome, so to speak. That idea will come up in later posts.
In this post, I will show you how you can solve a calculus problem without using calculus. Instead we will use Bayesian Optimization. The terminology for Bayesian optimization is simple. Generally, the process being optimized can be thought of as the "objective function". Like all functions, the objective function has input and output. The input to the objective function are the things that can be controlled (variables, parameters, hyper-parametes, etc). And the output of the objective function is the quantity that we wish to maximize or minimize.
I like to think of Bayesian Optimization as “finding when/where the derivative is zero” for something that does not necessarily have to be a mathematical function like the ones we were taught in school. I am always open to modifying this interpretation, but as of now, this makes total sense to me.
You may be asking, so why is finding when/where the derivative is zero important anyways? The place where the derivative equals zero is a local extrema in the original function. Or in other words, it tells you the location at which there is a local maximum/minimum in the original function. That property allows us to to solve optimization problems. However, with both Calculus and Bayesian Optimization, it is possible to get stuck in a local extrema rather than finding the true global maximum/minimum.
So what are some things we can optimize? How about an automated investment simulation? Imagine having an automated investment system that optimizes itself in real time. Now that would be valuable right?
We will now solve a Calculus problem from this blog post using Bayesian Optimization to reinforce what I mean by “finding when/where the derivative is zero”. The problem in this post is to minimize the cost of material used to make a soda can. There are three things to consider before solving this problem using hyperopt:
1: The volume of the can is constant. V=355cm^3
2: To minimize cost, we must minimize surface area and thus reduce the amount of material used.
3: To reduce computational time, the area function should be in terms of a single variable (r or h)*
*This is not necessary, but will drastically reduce “optimal parameter search time”. I will go over why at the end of this post. Also, notice how it was necessary to define the surface area in terms of a single variable for the calculus solution.
All of the algebra used for finding the area function are documented in this blog post . Once you have reduced the area of the can to a single variable function, you can use calculus like in the blog post, or you can use an optimization algorithm. The former is an analytical method while the latter is a numerical method.
The Python code below will solve the problem from this blog post using Bayesian Optimization and print the answer. One cool thing to note is that an understanding of calculus is not necessary to write this code. You simply create your objective function, “surface_area()” in this case. Then, you define your search space, only a single variable “r” from a uniform distribution in this case. Finally, you specify the parameters inside of the function “fmin()” and voila. Sit back and wait for the computer to do all the hard things for you.
import math
from hyperopt import fmin, tpe, hp, Trials
V = 355
def surface_area(params):
h = V / (math.pi*params['r']**2)
A = 2*math.pi*params['r']**2 + 2*math.pi*params['r']*h
return A
space = {
"r": hp.uniform("r", 0, 5),
}
tpe_algo = tpe.suggest
tpe_trials = Trials()
tpe_best = fmin(fn=surface_area,space=space,algo=tpe_algo,trials=tpe_trials,max_evals=500)
print("The optimum radius is:")
print(f"{tpe_best['r'].round(4)}cm")
print("The optimun height is:")
print(f"{(V / (math.pi*tpe_best['r']**2)).round(4)}cm")
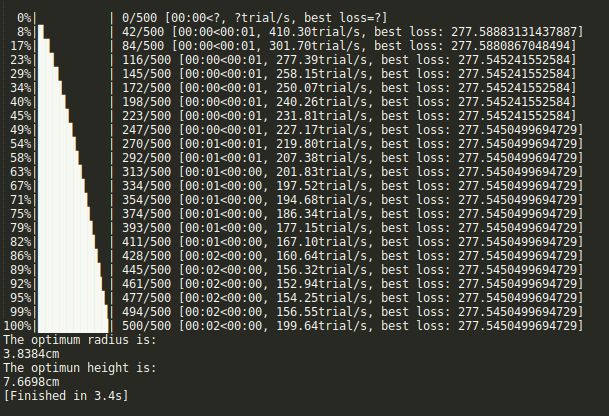
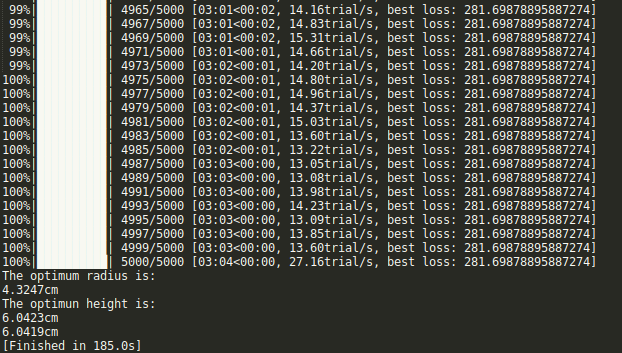
Now lets talk about why having the area defined in terms of a single variable is desirable, but not entirely necessary. You have the ability to define a multi-dimensional search space with hyper opt. Theoretically you can define as many variables as you want in the search space. However, the more variables you define, the more computational power/time it will take. Notice how in the output above the code finnished in 3.4 seconds. When we add one more variable to the seach space, the computational time increases to 185 seconds and the solution is only close to the correct solution. See the output below.
The Python code below will solve the problem from this blog post , but the area function is now a function of two variables. Notice how there is now some logic within the objective function. This is necessary because “h” is no longer defined before “A” is calculated. Also, notice how the “max_evals” parameter is so much larger than before. This is necessary because it has to check so many more possible solutions than the previous example with the extra variable defined in the search space.
import math
from hyperopt import fmin, tpe, hp, Trials
V = 355
def surface_area(params):
A = 2*math.pi*params['r']**2 + 2*math.pi*params['r']*params['h']
if math.pi*params['r']**2*params['h'] > 355 and math.pi*params['r']**2*params['h'] < 355.5:
return A
else:
return 1000
space = {
"r": hp.uniform("r", 0.001, 5),
"h": hp.uniform("h", 0.001, 10)
}
tpe_algo = tpe.suggest
tpe_trials = Trials()
tpe_best = fmin(fn=surface_area,space=space,algo=tpe_algo,trials=tpe_trials,max_evals=5000)
print("The optimum radius is:")
print(f"{tpe_best['r'].round(4)}cm")
print("The optimun height is:")
print(f"{tpe_best['h'].round(4)}cm")
If you have made it this far, then congratulations! We went from a brief description of Bayesian Optimization to seeing it used in a real problem. I hope this post got you excited because there are so many tools just sitting around waiting to be used. Hyperopt is just one of them.